本文共 2230 字,大约阅读时间需要 7 分钟。
Python实现插入排序
一、插入排序简介
插入排序(Insertion Sort),也被称为直接插入排序,是一种常见的排序算法。
插入排序是将元素列表中未排序的数据依次插入到有序序列中。从元素列表的第一个数据开始(将第一个数据视为已排序序列),按顺序将后面未排序的数据依次插入到前面已排序的序列中。对每一个未排序数据进行插入,是将该数据依次与相邻的前一个数据进行比较,如果顺序错误则交换位置,直到不需要交换则该数据插入完成。
插入排序的原理类似于玩扑克牌时,手动抓牌和排序,每抓一张新牌都按顺序插入到已有的牌中。
二、插入排序原理
插入排序的原理如下:
1. 将待排序列表的第一个元素当做已排序序列,第二个元素到最后一个元素当成未排序序列。
2. 取未排序序列中的第一个数据,插入到已排序序列中顺序正确的位置。将未排序的第一个数据与相邻的前一个数据(已排序序列的最后一个数)据进行比较,如果顺序错误则交换位置,交换位置后继续与相邻的前一个数据进行比较,直到不需要交换则插入完成。每次插入数据后,已排序序列都是排好序的。
3. 重复上一步,继续插入下一个数据。每进行一次插入,已排序序列的长度加1,未排序序列的长度减1,直到列表中的所有数据都插入到已排序序列了,则列表排序完成。
以列表 [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21] 进行升序排列为例。列表的初始状态如下图。

要进行升序排列,则每次插入一个数据后,已排序序列都是升序排列的。
1. 将第一个数据当成已排序序列,后面的数据当成未排序序列。取未排序的第一个数据与已排序的最后一个数据进行比较,如果顺序错误则交换位置。17(未排序的第一个数据)比10(已排序的最后一个数据)大,不需要进行交换。

2. 当不需要交换时则此轮插入完成。已排序序列变成了两个数据,未排序序列数据减1。
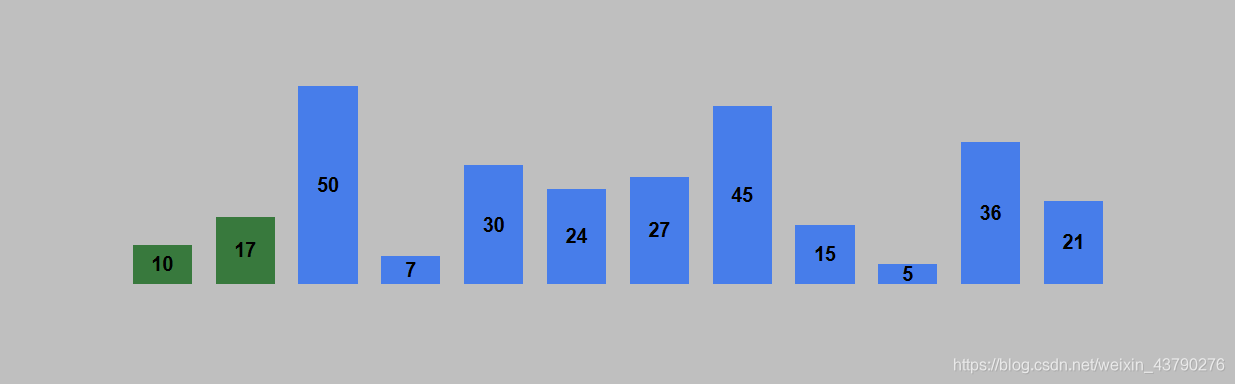
3. 继续取未排序的第一个数据与已排序的最后一个数据进行比较。如果顺序错误则交换位置。50比17大,不需要交换。
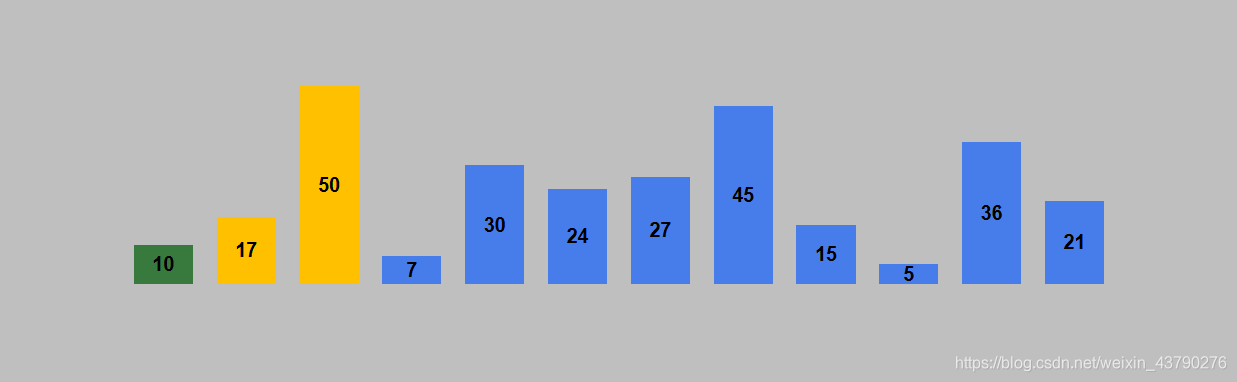
4. 第二轮插入完成,已排序序列数量加1,未排序序列减1。
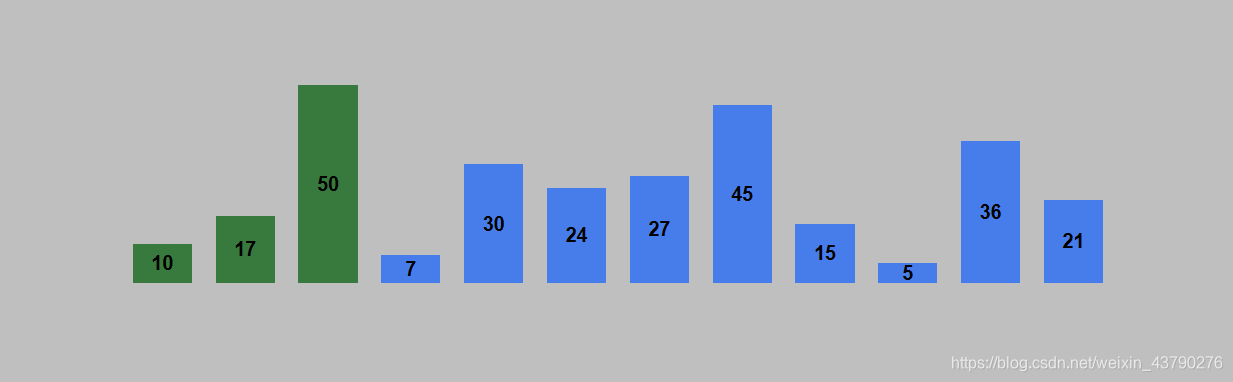
5. 重复上面的步骤,未排序的第一个数据与已排序的最后一个数据进行比较。

6. 如果位置错误则交换位置。 7比50小,交换位置。

7. 交换位置后,继续将插入的数据与相邻的前一个数据进行比较。
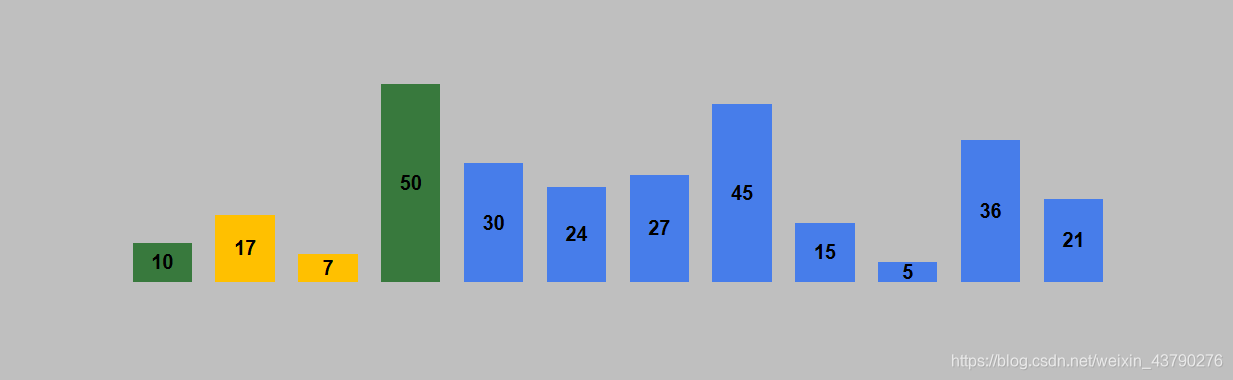
8. 如果位置错误则交换位置。 7比17小,交换位置。
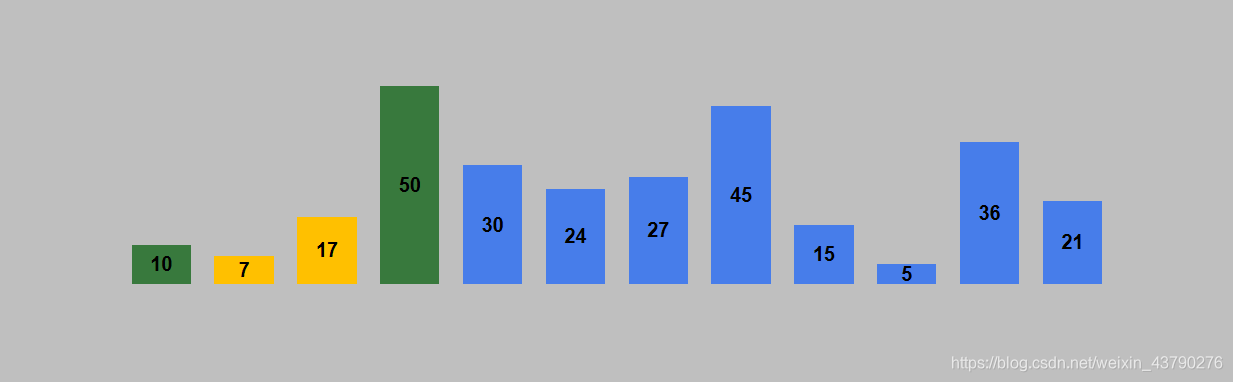
9. 重复步骤7,继续将插入的数据与相邻的前一个数据进行比较。
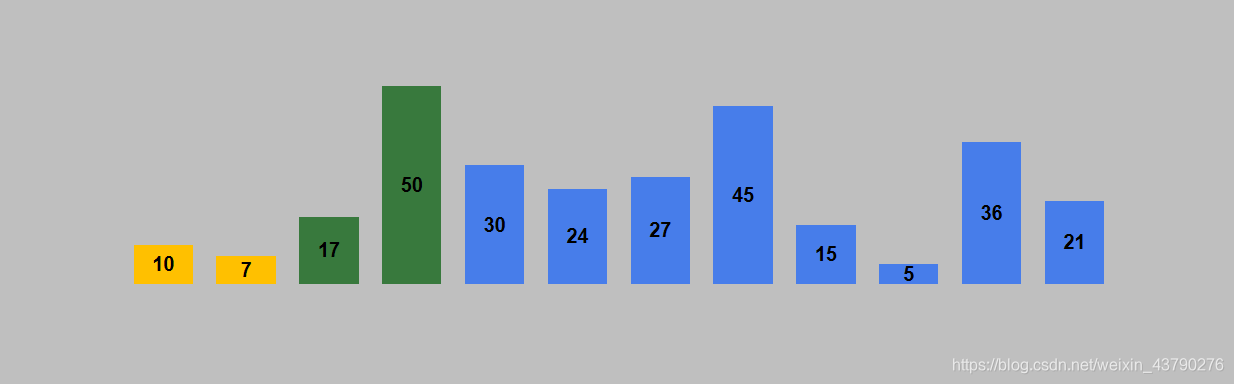
10. 如果位置错误则交换位置。 7比10小,交换位置。此时插入的数据已经通过交换位置到达了数列的最前端,不需要再次交换了,此轮插入完成。

11. 一直重复取未排序的第一个数据插入已排序序列中,直到所有数据都已经插入到已排序序列中,列表排序完成。排序结果如下图。

三、Python实现插入排序
# coding=utf-8def insertion_sort(array): for i in range(len(array)): cur_index = i while array[cur_index-1] > array[cur_index] and cur_index-1 >= 0: array[cur_index], array[cur_index-1] = array[cur_index-1], array[cur_index] cur_index -= 1 return arrayif __name__ == '__main__': array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21] print(insertion_sort(array))
运行结果:
[5, 7, 10, 15, 17, 21, 24, 27, 30, 36, 45, 50]
代码中,i 表示取列表中索引为 i 的数据进行插入排序(相当于“抓牌”),使用 cur_index 标记待插入数据向前移动时的索引,直到不需再移动(相当于将新抓的牌插入到已有的牌中),当列表中的所有数据都插入到了已排序序列中,列表排序完成。
四、插入排序的时间复杂度和稳定性
1. 时间复杂度
在插入排序中,最坏的情况是元素列表的初始状态是完全逆序排列的,每一轮插入都需要移动到最左端,需要进行 n-1 轮“插入”,每一轮“插入”需要向前比较和移动 i 次,i 的平均值为 n/2 ,时间复杂度为 T(n)=n(n-1)/2 ,再乘每次操作的步骤数(常数,不影响大O记法),所以插入排序的时间复杂度为 O(n^2) 。
在插入排序中,当待排序列表有序时是最优的情况,只需将待插入数据跟前一个数据比较一下就可以了(都不需要交换),共需要比较 n-1 次,时间复杂度为 O(n) 。所以,插入排序适用于有部分数据已经排好序的情况,并且排好序的部分越大越好。
对于数据量少的排序,它是一个很好的排序算法,一般在数据规模大于1000的场合下不建议使用插入排序。
2. 稳定性
在插入排序中,每次将一个未排序的数据插入到已排序序列中,插入的方式是从后到前依次比较和交换,如果元素列表中有两个相等的元素,不会进行交换,相对次序是保持不变的。所以插入排序是一种稳定的排序算法。

转载地址:http://czppz.baihongyu.com/